$\delta$ Capítulo 2 - Seção Exercícios (pág. 151 a 153)

Questão 04 - José Hudson

Solução:

Questão 07 - Jailson Bezerra

Solução:

Questão 10 - Diana Keli

Solução:

Questão 17 - Guilherme Oliveira

Solução:

Questão 22 - Val Maia

Solução:

Questão 24 - Thales Fernandes

Solução:

Questão 25 - Robson Santos

Demonstre cada afirmação usando a definição precisa de limite.

$\displaystyle  \lim_{h\rightarrow 2}(14-5x)= 4$

Solução:

Dado $\displaystyle   \varepsilon > 0$  , precisamos comparar $\displaystyle  \delta > 0$  de modo que  $\displaystyle   0 <|x-2 |<\delta$ , então  $\displaystyle  |(14- 5x)- 4| <\varepsilon$. Mas $\displaystyle  |(14- 5x)- 4| < \varepsilon \Leftrightarrow |-5x + 10| < e \Leftrightarrow  |-5| |x- 2| < e \Leftrightarrow  | x- 2| < \varepsilon /5$.  Então , se escolhermos $\displaystyle  \delta  = \varepsilon /5$ , então $\displaystyle   0 < |x- 2| < \delta  \Rightarrow |(14-5x)- 4| <\varepsilon$ . Portanto , $\displaystyle  \lim_{h\rightarrow 2}(14-5x)= 4$ é a definição do limite.

Questão 27 - Alessandra Farias

Solução:

Questão 28 - Jailson Bezerra

Solução:

Questão 29 - Alessandra Farias

Solução:

Questão 30 - Thales Fernandes

Solução:

Questão 31 - José Hudson

Solução:

Questão 33 - Diana Keli

Solução:

Questão 35 - Robson Santos

(a) Encontre a inclinação da reta tangente à curva y = 9 - 2 x² no ponto (2,1).

(b) Encontre uma equação dessa reta tangente.

Solução:

A_

A inclinação da reta tangente em (2,1) é :

$\displaystyle  f'(x)= \lim_{h\rightarrow 2}\frac{f(x)-f(2)}{x-2}$

$\displaystyle f'(x)= \lim_{h\rightarrow 2}\frac{9-2x^2-1}{x-2}$

$\displaystyle f'(x)= \lim_{h\rightarrow 2}\frac{8-2x^2}{x-2}$

$\displaystyle  f'(x)= \lim_{h\rightarrow 2}\frac{-2(x^2-4)}{x-2}$

$\displaystyle  f'(x)= \lim_{h\rightarrow 2}\frac{-2(x-2)(x+2)}{x-2}$

$\displaystyle  f'(x)= \lim_{h\rightarrow 2}{[-2(x+2)}] = -2 \cdot4 = -8$

B_

A equação dessa reta tangente é :$\displaystyle$$y- 1 = -8(x- 2)$ ou $y = -8x + 17$

Questão 36 - Aline Cristina

Solução:

Questão 38 - Marden Torres 

Solução:

Questão 40 - Val Maia

Solução:

Questão 43 - Guilherme Oliveira

Solução:

Questão 44 - Antônio Wagner

Trace ou copie o gráfico da função. Então, esboce o gráfico de sua derivada.

Solução:

Questão 46 - Antônio Wagner

a) Encontre as assíntotas do gráfico de $f(x)=\displaystyle\frac{4-x}{3+x}$ e use-as para esboçar o gráfico.

Solução:

como x tende ao infinito, $f(x)=\displaystyle\frac{4-x}{3+x}$ tende -1, então há uma assintota horizontal em y = -1. x tende 3^+, f(x) tende ao infinito, e como x tende a -3^-, f(x) tende ao infinito. Assim existe uma assintota vertical em x=3.

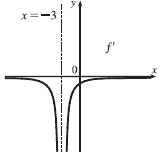
b) Use o gráfico da parte (a) para esboçar o gráfico de f'.

c) Use a definição de derivada para encontrar f'(x).
$f'(x)=lim\limits_{h \to 0}\displaystyle\frac{f(x+h)-f(x)}{h}$
$f'(x)=lim\limits_{h \to 0}\displaystyle\frac{4-(x+h)-4-x}{3+(x+h)-3+x}$
$f'(x)=lim\limits_{h \to 0}\displaystyle\frac{(3+x)[4-(x+h)]-(4-x)[3+(x+h)]}{h(3+x(x+h)(3+x)$
$f'(x)=lim\limits_{h \to 0}\displaystyle\frac{(12-3x-3h+4x-x^2-hx)-(12+4x+4h-3x-x^2-hx)}{h[3+(x+h)(3+x)}$
$f'(x)=lim\limits_{h \to 0}\displaystyle\frac{-7h}{h[3+(x+h)](3+x)$
$f'(x)=lim\limits_{h \to 0}\displaystyle\frac{-7}{3+(x+h)(3+x)$
$f'(x)=lim\limits_{h \to 0}\displaystyle\frac{7}{3+x}^2$

Questão 50 - Marden Torres

Solução: